Constructive and Destructive Wave Interferences

So we've learned about waves recently. And it's more...geometric then I thought.
There are apparently two types of wave interferences, and you can probably guess what they are from the title.
Firstly, the basic parts of the wave is as shown:

When two waves from each side collides with each other, they combine with each other. Two waves colliding in the same direction vertically is called a constructive interference. It's when the waves involved is a crest and a crest, or a trough and a trough. When they meet, the shapes of the waves combine on top of each other, and then they go back on their seperate ways.

When the two waves of different directions vertically collide, it is called a destructive interference. This would be when a trough and a crest are involved. These two combine as well, but one negates another.

Different Types of Energy

OH YEAH. Energy.
Makes me think of Dragon Ball Z and YEAHHHHHH.
I LIKE.
ENERGY.
BECAUSE IT'S ENERGY.
Ok. So I gotta blog about the six different types of energy. And here they are.

First type is chemical energy. As the name suggests, it's the energy of chemicals. To be more specific, the atoms of covalent bonds are held together by chemical energy. When these chemicals react, it either releases or absorbs heat. They are called exothermic and endothermic, respectively.
Second is gravitational potential energy. This is the energy that increases due to its position in gravitational field.
Another is elastic potential energy. This is energy from deformation of elastic objects, such as springs. This force is equal to the work done on the spring to stretch it.
Mechanical energy has two types: potential and kinetic. Mechanical kinetic energy is the energy of motion on an object through applied force.
Thermal energy is the kinetic energy of the atoms and molecules' random movements.
Lastly, sound energy is the energy caused by vibrations of atoms through mechanical energy, not resulting in any chemical change.

Cannons

http://www.youtube.com/watch?v=bSdHUOBNm68
Is it bad if that's the first thing that came into my mind when the teacher said we were gonna make a cannon?

So we were to make a cannon out of 5 pop cans. Three for nuzzle, two for base, and a pair of styrofoam cups for a projectile. It'll be fueled by ethanol. Our goal was to make the projectile travel as far as possible.

http://hyperphysics.phy-astr.gsu.edu/hbase/traj.html
According to this site, projectiles travel farthest at 45 degrees, assuming there's nothing in the way.

We also learned that according to Newton's Law, acceleration = force/mass, so we'd want to make the cannon heavy as possible if we don't want it to fly away when we launch it.

Newton's Laws of Force: Four Problems

HEYYYY guys. It's been a while. Did you miss me? I sure as hell did -coughdidn'tcough-

Anyway, it's time for another blog. This time it's about the four problems based on Newton's laws of force that we learn in grade 11 physics. First, let's get to the three laws.

Newton thought of three laws to explain how forces work in the world. They are:
-Law of inertia: object will maintain their motion (stationary or moving) unless there's an external force acting on it.
-Relationship between force, mass and acceleration: Force is directly proportional to acceleration, and mass is inversely proportional to acceleration. Therefore, a=F/m.
-For every action, there's a reaction of equal and opposite strength.

Now that we know the three laws, let's get on to the problems:
Equilibrium:

Equilibrium problems usually consist of two forces acting on an object that keeps it stationary. Therefore, the net force would equal to zero. In order to solve the problem, we must list a few assumptions.
-no friction
-no air resistance
-positive areas
-Fnet = 0, a = 0
-rope is weightless
Now, from Newton's second law, we know F = ma. To find the Fx, we do this:
Fx = max
Fx = 0
T1x - T2x = 0
T1x = T2x
T1cosθ = T2cosθ
T1 = T2
With this information, we can solve Fy.
Fy = ma
Fy = 0
-Fg + T1y + T2y = 0
T1y + T2y = Fg
T1sinθ + T2sinθ = mg
Then we can single out any part of the formula, and figure out the missing value.

Incline:

There are two types of inclines, static and kinetics. Static is when the object is not moving, and kinetic is when the object is moving.
They have different assumtions.
Assumptions (Static):
-fs
-Fn is perpendicular to the surface
- a = 0
- positive in the direction of acceleration.
- no air resistance
We would solve like this:
Fx = 0
Fgx - fs = 0
Fgx = fs
mgsinθ = muFn  *
Fy = 0
Fn - Fgy = 0
Fn = Fgy
Fn = mgcos θ  *
now put the *s together:
mgsinθ = mu(mgcosθ)
mu = sinθ/cosθ
mu = tanθ
and now you can find out what you need.
Assumptions (kinetics):
-fk
-Fn is perpendicular to surface
- ax ≠ 0, ay = 0
- positives in the direction of acceleration
- no air resistance
To solve:
F= ma
Fy = 0
Fn - Fgy = 0
Fn = Fgy
Fn = Fgcosθ
Fn = mgcosθ  *
Fx = max
Fgx - fk = max
Fgsinθ - muFn = max
insert * into above
mgsinθ - mumgcosθ = max
And now we can single out and figure out whatever we need.

Pulleys:

Assumtions:
-frictionless pulley and rope
-no air resistance
-multiple Free Body Diagrams
-positives in the direction of acceleration
- T1 = T2
- acceleration of system is the same.
To solve:
F = m1a
Fy = m1ay
m1g-T = m1a
The x components cancel out as there isn't Fx or ax.
F = m2a
Fy = m2ay
T - m2g = m2a
Fx again cancels out for the same reasons.
to find T and a
m1g - T = m1a     *
T - m2g = m2a    @
From *, T = m1g - m1a   #
from @, T = m2a + m2g  $
set # = $   m1g - m1a = m2a + m2g
m2a + m1a = m1g - m2g
a(m2 + m1) = m1g - m2g
a = m1g - m2g / m2 + m1
Then we find the a. To find T, sub a into # ( T = m1g - m1a).

Trains:

God I miss my tablet. And PaintoolSai. MS Paint and mouse is just annoying.

Assumptions:

- 3 Free Body Diagrams to find T

- no air resistance

- ay = 0

- cables are weightless

- positive in direction of a

- a is constant

- horizontal

To solve:

F = mta

Fy = 0

Fn - mtg = 0

Fn = mtg  *

F = mtax

Fa - f = mtax

Fa - muFn = mta

Fa - muFn/mt = a

and we find the acceleration.

F = ma

Fy = 0

Fn - m3g = 0

Fn = M3g  *

F = m3ax

T2 - f3 = m3ax

T2 - mum3g = m3a

T2 = m3a + mu m3g

and we find the T2.

F = ma

Fy = 0

Fn - m2g = 0

Fn = m2g  *

F = m2ax

T1 - T2 - f2 = m2ax

T1 - T2 mum2g = max

T1 = m2ax + T2 + mum2g

And we find the T1.

What a handful to do. Lot of them seems repetitive but it'll come in handy in the future when the questions become more complicated, apparently.

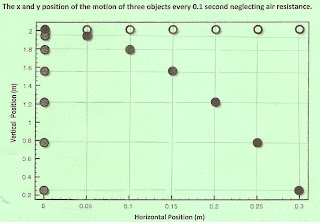
Projectile Motion

Ohhh yeah. Time to do some work with throwing stuff. That's the best science there is.

The basics of projectile motion would be to learn about the x and y vector components of the projectile. Remember vectors? From a few blogs ago? Yeah those things.
Here's a diagram of a type one projectile motion, which is a falling object:

We first need to remember that Vx is always constant, so there is no acceleration. Or at least in this unit so far. In real life, there would be stuff like air resistance changing the Vx, but we won't go there yet.
Vy is affected by gravity from V1y = 0, and therefore Ay would be gravity. Gravity is 9.8 m/s^2, unless stated otherwise. You could be throwing a ball on the moon or something. I don't know what astronauts like to do in their spare time but ok. We should also remember, time is equal to both Vx and Vy. Distance of y would be the height of whatever it's falling from, and Dx would be VxT. That covers about the basics of the falling object.

Now let's take a look at the other type of projectile motion:

Vx is still constant in this case, again at least until up to this point of the unit. So Ax is still zero as well. What's different is that this time, we might have to find the Vx using the angle and initial velocity given, using the SOHCAHTOA thing again. This might be switched and we might have to find the angle using Vx, etc. Vy is effected by gravity again, but this time, gravity has a negative value of -9.8 m/s^2. This is because this time, there is a negative and positive direction of y, so gravity's direction needs to be specified or the numbers will be wrong. Again, we can find Vy using SOHCAHTOA like Vx. Also, in this case Dy = 0, since there has been no vertical displacement. At the highest point of the motion, represented by H, Vy = 0. The time is known as hang time in this situation, which we calculate by using one of the Big 5 equations, d = V1t + 1/2(gt^2).

There are actually two more types of motions, where the ball actually lands on a higher or lower ground from the beginning in the second type of projectile motion. In these cases, they would have a positive or negative value of Dy.

Wonderland Coasters

Look at these things.

IF ONLY IT COULD CARRY FIREBALLS INSTEAD OF NORMAL ONES.

Oh dear lord I wish I was whoever created this thing. This is what I call creativity.

I-I love things based on stuff like playing cards or chess. This makes me happy inside.

And now we have to do one of these.

Ohhhh dear lord.

Vectors

ARRRRRRRRRRRRRRG HAPPY HALLOWEEN EVERYONE I TOTALLY DIDN'T FORGET TO BLOG BECAUSE MY MIND WAS OCCUPIED WITH HOLIDAY SPIRIT.
VECTORS. RIGHT.

SO. What happens with vectors is that we want to ADD THEM. Why? Because they're silly little things that tells you the direction by being SEPERATE so they can annoy you until you start pulling your hair out and head desk yourself.

OK not really they're basically lengths of directions, which can go North, South, East, West. They can also be known as North and negative North, East and negative East and vice versa, whatever is easier for you.

So when you get seperate vectors, you'll want to add them in order to see the sum of the vectors. If you don't get why, imagine you're trying to find a way to get to a destination the quickest. So for example, if you were given two vectors like 3 to North and 5 to South, the quickest way to get to the final point would be 2 to South. This is the sum of our vectors.

What if we get more then one dimention? Like 2 to the North and 5 to th East? Then we're going to have to use the Pythagorian Theorum. Oh yeah, more math, who's excited? I sure am not. If you try sketching the vectors, you might notice something.

That's right, the right angle triangle. So you can find out the total vector by adding the squares of the lines, then square rooting it. So it would be 2² + 5² = R², R = 5.39.

We can also find the angle of the vector so we know the exact direction. We do this by using trigonometry. Oh HEY there, SOH CAH TOA, long time no see. Here's a diagram of how we're going to use this:

The guy with the Zs and the angles are here too, joy. We want to use TOA, so it would be tan(data) = opp/adj = 2/5, (data) = tan^-1 (2/5), (data) = 21.8.
Finally, we would display the answer like this: 5.39 units [N 21.8^o E]. Well that's all folks, have a happy halloween that's over in half an hour. Good night.